「ゼロから作るDeep Learning ① (Pythonで学ぶディープラーニングの理論と実装)」
p.129～132の写経です。
基本は、上流からの値と偏微分の乗算
まず、
を計算グラフで表すと、下図の通りです。
次に出力値であるEからの逆伝播は、偏微分との乗算で得られる為、
朱書きのようになります。
応用例? 合成関数での逆電波
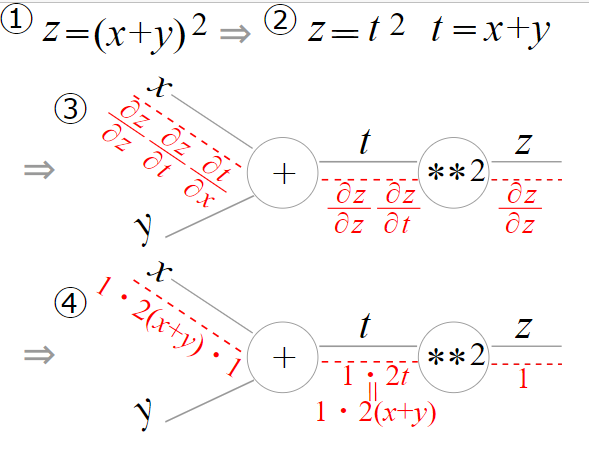
今度は、[tex: \large{z=(x+y)2}]の場合を考えます。
この式は、下図の①→②のような合成関数へ置き換えることができますので、
下図のような計算グラフで表すことができます。
逆伝播は、上流の値と、偏微分の乗算で得られますので、
下図の朱書きのようになります。
