pythonによる数値微分

勾配降下法に向け、o'reilly「ゼロから作る Deep Learning」の4章を写経.

github.com

以下のscriptは

を

のように数値微分しています

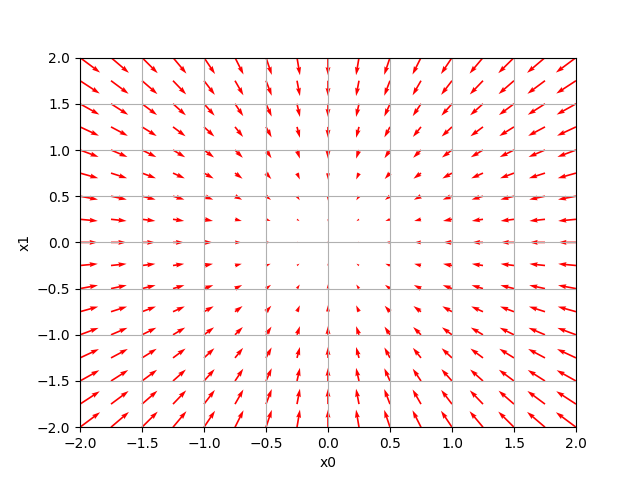
#!/usr/local/bin/python
# -*- coding: utf-8 -*-

# https://github.com/oreilly-japan/deep-learning-from-scratch
# http://d.hatena.ne.jp/white_wheels/20100327/p3

import numpy as np
import matplotlib
matplotlib.use('Agg')
import matplotlib.pylab as plt

from mpl_toolkits.mplot3d import Axes3D


def main():
    # 等差数列の作成 (start, stop, step)
    x0 = np.arange(-2, 2.5, 0.25)
    x1 = np.arange(-2, 2.5, 0.25)
    # 格子座標の作成ｋ
    X, Y = np.meshgrid(x0, x1)
    # 1次元化
    X = X.flatten()
    Y = Y.flatten()

    # 数値微分
    grad = numerical_gradient(function_2, np.array([X, Y]) )
    

    plt.figure()
    #ベクトルの描画
    plt.quiver(X, Y, -grad[0], -grad[1],  angles="xy",color="#ff0000")
    plt.xlim([-2, 2]) #表示範囲
    plt.ylim([-2, 2])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()
    plt.draw()
    plt.savefig( 'numerical_gradient.png' )


# 数値微分
def numerical_gradient(f, X):
    if X.ndim == 1:             # ndim: 次元数
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X) # X と同じ形状の「0 配列」作成
        
        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)
        
        return grad


# 数値微分(詳細?) ...  dy/dx = lim(h->0) { f(x+h) - f(x-h)} / 2h }
def _numerical_gradient_no_batch(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)   # X と同じ形状の「0 配列」作成
  
    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)
        
        x[idx] = tmp_val - h
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val # 値を元に戻す
        
    return grad


def function_2(x):
    if x.ndim == 1:   # ndim: 次元数
        return np.sum(x**2)
    else:
        # numpy.sum() の axisは次のurl参照
        # https://deepage.net/features/numpy-axis.html
        return np.sum(x**2, axis=1)


# def tangent_line(f, x):
#     d = numerical_gradient(f, x)
#     print(d)
#     y = f(x) - d*x
#     return lambda t: d*t + y


if __name__ == '__main__':
    main()

↑こう書くと、↓こう表示されます